As I’ve stated before, circle area would once again be investigated. This iteration brings uniform sub-intervals into play (apologies for all the color but thought it would be helpful for students to distinguish upper and lower bounds). The link directly below this image opens a new tab from which students can adjust two parameters to explore the partitions; those sliders appear at the right-hand side near the bottom.

In the image above, there are two rectangles displayed; the length of the blue rectangle is based on the circumference of the upper bound, the length of the red on the lower bound. By reducing the width of each partition (link below), you will see that these two lengths approach a common value.
Interactive exploration of the image directly above.

For a direct comparison between this version and that using non-uniform partitions, I’ve added the image below.

One final note here: Area of the circle using annuli of uniform sub-intervals extends naturally to volumes by cylindrical shells. Walls extend perpendicular to the upper and lower bounds of each annulus; the height of these walls is governed by a function of “x” (single variable calculus). For f(x)=c, the layering effect of cylindrical shells forms a cylindrical solid. For f(x)=ax+c, the solid formed is a cone, if f(x)=ax^2+b, a paraboloid emerges. These are a reasonable conclusions that high school students readily accept. Volumes by slabs follow the same argument.
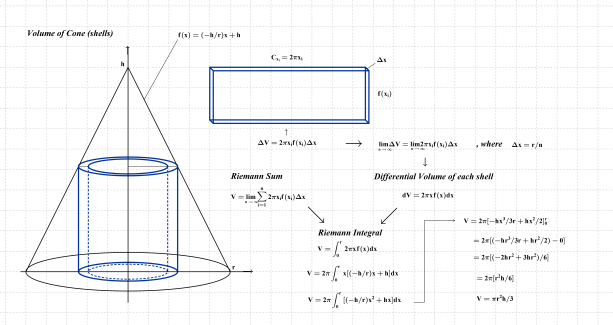
I also like to have students set up integrals from both dx & dy perspectives (as seen below).

Thanks for reading.
