Archive for the ‘Related Rates’ Category

Related Rates: Ball Drop & Shadow

Posted: March 13, 2016 in Calculus: An Introduction, Differential Calculus, Differential Equations, Related Rates
Tags: ,
0

Here’s problem involving a falling object and the speed at which its shadow travels along the ground. As usual, in related rates, once a relationship between the variables involved has been established, the calculus required to reach its conclusion is very straight forward.

In order to make efficient use of time, these problems provide students the opportunity to practice simple differentiation procedures. In addition, the graphs provided below open the door to a discussion on the Mean Value Theorem of differential calculus, serving to either introduce or reinforce that concept.

 

Falling Ball

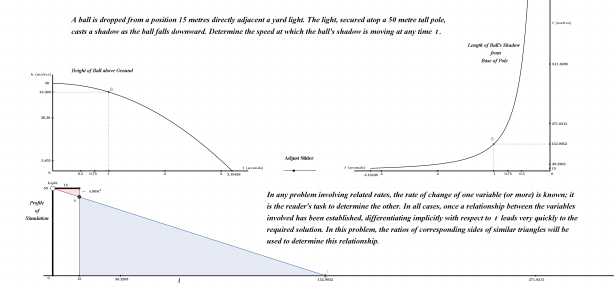
RelatedRatesBallDrop

Click on the link provided here to interact with the falling ball and its shadow.

 

 

The ball’s displacement from its release point was provided in the image above. As a review (since integral calculus has already been introduced), that displacement formula is once again derived through basic differential equations; this is shown directly below.

Acceleration, Velocity and Displacement

BallDropDisplacementFormula

 

I’ve included solutions for  t=1  and  t=2  below. In keeping with my belief that students can learn effectively through comparison and contrast, three varied methods are shown.

Solutions

RelatedRatesBallDropSolutions

Thanks for reading.

Related Rates (continued)

Posted: March 1, 2016 in Calculus: An Introduction, Differential Calculus, Differential Equations, Implicit Differentiation, Related Rates, The Derivative
Tags:
0

In the spirit of consistency, several additional examples supplementing my introduction to related rates are included here. As seen in the first example below, past concepts are revisited and, in turn, connected to newly introduced ones. Mixing things up from that point on provides students with a variety of perspectives on the same theme that serves to further cement understanding.

 

Separable Differential Equation

Circle area Derivative

 

Three Approaches to Related Rates

Circle area Differential Equation

 

Application to Conical Container

DiffEqua Realted Rates2

 

 

Rate of Change of Arc Length

DiffEquaRelatedRatesArcLength

 

The approach to solving each of these related rate problems is the same; identify what is known, what is desired and then connect the two.

 

Thanks for reading.

Related Rates

Posted: February 29, 2016 in Calculus: An Introduction, Differential Calculus, Related Rates
Tags:
0

Most related rate problems that high school students see involve three variables. The way in which things unfold usually goes as follows: One rate of change is given, the task being to find another. With three variables in the mix, the typical approach is to find a direct relationship between two of those variables and then express one in terms of the other. The third variable is then be expressed in terms of one variable only, and away we go.

There are cases, however, when all three variables must stand on their own as no direct relationship exists between any two. In such cases, two rates are provided while finding the third rate remains the goal.

The example shown below has a trough filling at a constant rate of 2 cubic feet per minute (dV/dt). The task is to determine the rate at which the depth (height) of water is changing (dh/dt) at any time. Since rates involving volume and height are directly involved here, the typical approach is to express volume in terms of height first and then differentiate. This approach (#1) will follow the image below. Since, however, I like to mix things up and provide alternative ways of thinking, a second approach will be included as well.

 

The Problem: Determine an expression for dh/dt.

 

V-Trough2

 

Approach #1

Related Rates 1

Approach #2

Related Rates 2

The first approach above is more direct in this case. Having said that, awareness of approach 2 will provide leverage to deal with problems in which two independent rates are provided. In those scenarios, the substitution leading to the final expression is not carried out. I included it in the example above to show that each approach yields the same result.

Follow the link provided here to see how the rate of change in depth changes as the trough fills.

Click on the link provided here for more related rates.

 

Thanks for reading.