Archive for the ‘Optimization’ Category

Inscribed Triangle: Maximum Area

Posted: March 11, 2016 in Calculus: An Introduction, Curve Sketching, Differential Calculus, Differential Equations, Optimization, The Derivative
Tags: , ,
0

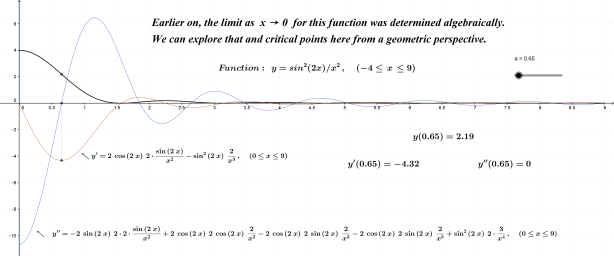
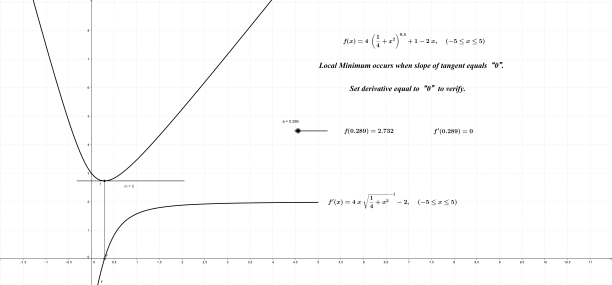
The main subject of this entry was originally planned as an optimization problem involving differential calculus only; its been slightly modified. This more interesting approach provides the derivative up front, presenting students with three separate tasks to pursue from that point. As a consequence, students are reintroduced to differential equations and curve sketching.

A talking point emerges as well: Is there a difference between derivatives and differential equations?

 

Inscribed Triangle of Maximum Area

Inscribed Triangle animation

 

Click on the link provided here to explore area of the inscribed triangle.

 

Thanks for looking.

Curve Sketching

Posted: March 3, 2016 in Calculus: An Introduction, Curve Sketching, Differential Calculus, Optimization, The Derivative
Tags:
0

By the time curve sketching is formally introduced, students have already seen a few “purposeful” examples; they are listed below as links.

–Putnam Problem, Four Towns, e^(Pi) vs (Pi)^e, f(x)=x^x (L’Hospital’s Rule)

Through these examples (and others), first and second derivatives have been points of discussion with respect to identifying the location and nature of critical points. In addition to this, L’Hospital’s Rule will have been established along the way and thrown into the mix.

My formal introduction to curve sketching is introduced in the form of a problem solving scenario. An example of this is shown below.

 

Sum of a Number and its Reciprocal

Curve Sketching

 

Limits at Infinity & Infinite Limits

Curve Sketching2

 

First and Second Derivatives

Curve Sketching3

 

Graph of   S(x) = x + 1/x

x + 1 by x

Click on the link provided to interactively determine the local extrema.

 

Graph of   y=sin^2(2x)/x^2  (see L’Hospital’s Rule for indeterminate limits of this function)

L Hospital's Rule Second Iteration2

Click on the link provided here to explore the relationships between  y, y’ and y”.

 

Thanks for reading.

Minimize Distance Connecting 4 Towns

Posted: January 12, 2016 in Differential Calculus, Optimization, The Derivative
Tags: ,
1

Four towns (A, B, C, D) are situated to form a square with side length of 1 unit. Determine the minimum length of roadway that will link these four towns together.

View the James Grime video first.

Minimum Length

Click on the following link for an interactive exploration: GeoGebra

 

The graph below shows the length of roadways linking these towns as a function.

Length as a Function of  “x”

Four Towns Minimum

Click on the link provided here to determine local minimum.

 

Thanks for reading.